Day Seven - Linearity and Superposition 3/23/2017

Today, we talked about linearity and superposition which can be used to solve complex circuit.
However, I thought it is more complicate than other circuit analysis method because it gives us multiple of circuits that we need to solve, but I also know that it is a convenient method to solve big and complex circuit.

First, we had our linearity problem. Note that as the Vs is doubled from 12 to 24, the current I also doubled because of the linearity property.

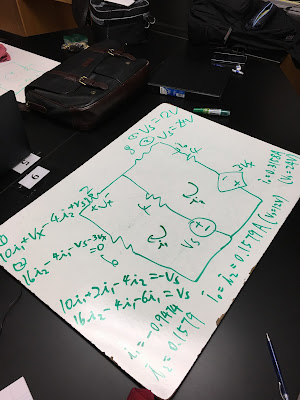
Here is the example of superposition. We first have to ignore all the independent sources except one. Then we use basic circuit analysis technique to solve for the voltage or the current that we need in the specific location. After that, we ignore the source we just use, and using another source as the source of the renewed circuit. Also calculate the voltage or current at the same specific location. Finally, we add up the contributions of both circuits at that specific location to get the actual value.

After that, we had our superposition lab.
Pre-Lab: we have to calculate the Voltage drop at the 6,8k resistor in the circuit above.
From our calculation, the voltage drop across the 6.8k resistor in the 3V voltage source circuit is 0.708V, and 1.99V in the 5V voltage source circuit. Adding up both contributions at the 6.8k resistor, we have 2.707 voltage drop across the 6.8k resistor,

Resistor Error:
9.8k(10k), 4.6k(4.7k), 0.975k(1k), 6.5k(6.8k), 21.7k(22k)

By measuring the voltage across the 6.8k resistor, we measured that 0.693V in the 3V voltage source circuit and 1.96V in the 5V voltage source. The sum of the voltage is 2.66V.
Combining both circuit, we have 2.65V of voltage drop across the 6.8k resistor.

Measured	Expected	Source
1.96volt	1.99volt	5V
0.693volt	0.708volt	3V
2.66	2.707	Total

Summary: I personally prefer other analysis techniques over superposition because it seems involving more circuit in the calculation than usual. However, this basic calculation using the linearity of the circuit can give us precise result on complex circuit, and this can be shown by the experiment.